Machine learning will definitely play a key role in designing algorithm optimization problems, with a focus on implementing the Platt SMO algorithm. The following article explores SVM optimization, primarily aiming to implement the Platt SMO algorithm to enhance the SVM model. It also attempts to use the GAFT genetic algorithm framework for initial SVM optimization.
**Heuristic Selection of Variables in SMO**
In the SMO algorithm, we need to select a pair of α values to optimize at each step. By using heuristic selection, we can more efficiently identify which variables to optimize, ensuring the objective function decreases as rapidly as possible.
Different heuristics are applied when selecting the first and second α values in Platt SMO.
**Selection of the First Variable**
The choice of the first variable is part of the outer loop. Instead of iterating through the entire α list as before, we now alternate between the full training set and the non-boundary samples:
First, we scan the entire training set to check for violations of the KKT conditions. If any αi and xi, yi violate the KKT condition, that point needs optimization.
The Karush-Kuhn-Tucker (KKT) conditions are the necessary and sufficient conditions for solving positive definite quadratic programming problems. For the SVM dual problem, the KKT conditions are straightforward:

After scanning the full training set and optimizing the corresponding α values, we then focus on the non-boundary αs in the next iteration. Non-boundary αs are those not equal to 0 or C. These points still need to be checked for KKT violations and optimized if necessary.
This alternating process continues until all α values satisfy the KKT conditions, at which point the algorithm terminates.
To quickly select the α with the largest step size, we cache the error values for all data points. A dedicated SVMUtil class was created to store important SVM variables and provide auxiliary methods:
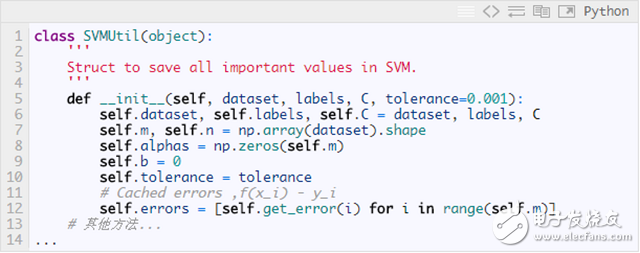
Here’s an approximate code snippet for the alternating traversal of the first variable. For the complete Python implementation, refer to: [https://github.com/PytLab/MLBox/blob/master/svm/svm_platt_smo.py](https://github.com/PytLab/MLBox/blob/master/svm/svm_platt_smo.py)

**Choice of the Second Variable**
The selection of the second variable in SMO is part of the inner loop. Once the first α1 is chosen, we aim to select α2 such that the change after optimization is significant. From our previous derivation:
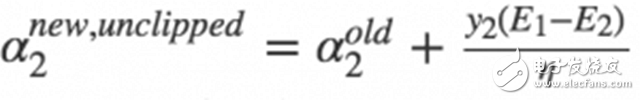
We know that the change in α2 depends on |E1 - E2|. When E1 is positive, we choose E2 as the smallest Ei. Typically, the Ei values of each sample are cached in a list, and we select α2 based on the maximum |E1 - E2|.
Sometimes, even this heuristic may not lead to sufficient improvement. In such cases, we follow these steps:
1. Select a non-boundary sample that causes a significant drop in the function value.
2. If none exists, select the second variable from the full dataset.
3. If still no improvement, reselect the first α1.
Here’s how the second variable is chosen in the Python implementation:
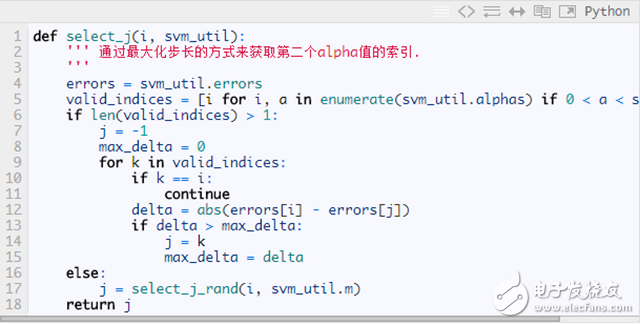
**KKT Conditions Allow for Certain Errors**
In the Platt paper, there is a tolerance allowed for the KKT conditions. Here's the corresponding Python implementation:

For the full implementation of Platt SMO, see: [https://github.com/PytLab/MLBox/blob/master/svm/svm_platt_smo.py](https://github.com/PytLab/MLBox/blob/master/svm/svm_platt_smo.py)
Using the Platt SMO algorithm on the previous dataset, we obtained the following result:

Visualizing the decision boundary and support vectors:
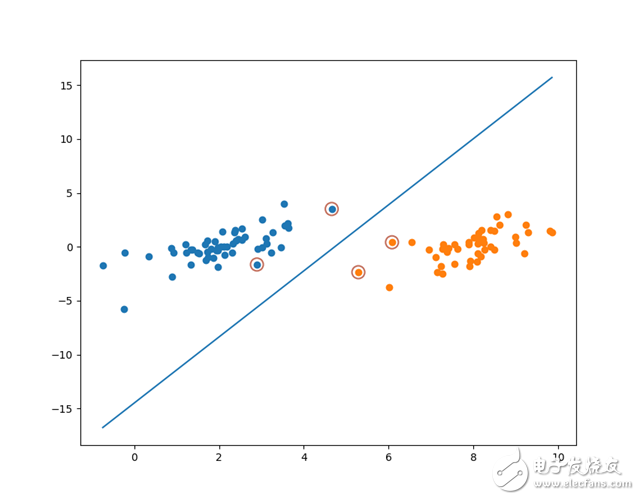
It can be seen that the support vectors optimized by Platt SMO differ slightly from those of the simplified SMO algorithm.
**Optimizing SVM Using Genetic Algorithms**
Since I recently developed a genetic algorithm framework, it's very easy to use it as a heuristic search algorithm. I tried applying it to optimize SVM.
Using a genetic algorithm allows us to directly optimize the original form of SVM, which is the most intuitive approach:
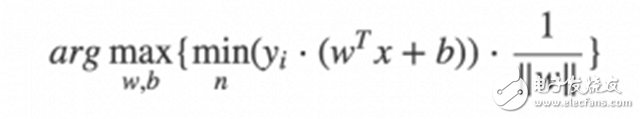
With the help of my own genetic algorithm framework, GAFT, I only needed to write a few lines of Python code to optimize the SVM algorithm. The most important part was writing the fitness function. Based on the above formula, we calculated the distance from each data point to the decision boundary and returned the minimum distance for evolutionary iteration.
GAFT project address: [https://github.com/PytLab/gaft](https://github.com/PytLab/gaft), please refer to the README for details.
We started building the population for evolutionary iterations.
**Creating Individuals and Populations**
For two-dimensional data points, we only need to optimize three parameters: [w1, w2] and b. The individual definition is as follows:

A population of a certain size was created.

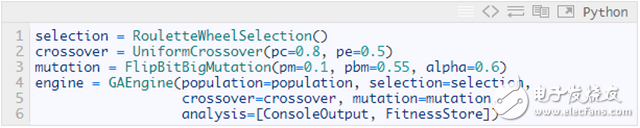
**Creating Genetic Operators and GA Engines**
Nothing special here—just use the built-in operators from the framework.
**Fitness Function**
This part just involves describing the original form of SVM. It only takes three lines of code:

**Starting the Iteration**
We ran the population for 300 generations.

Plotting the decision boundary optimized by the genetic algorithm:
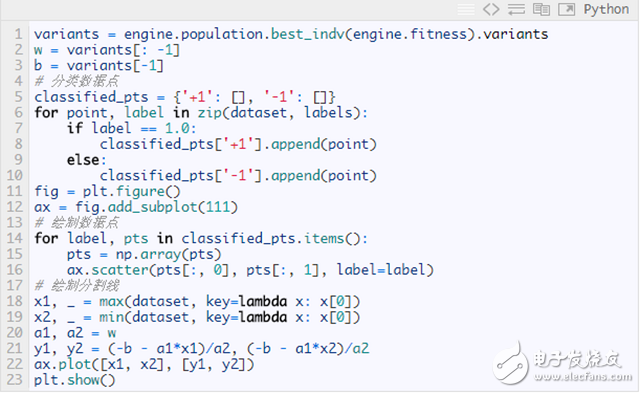
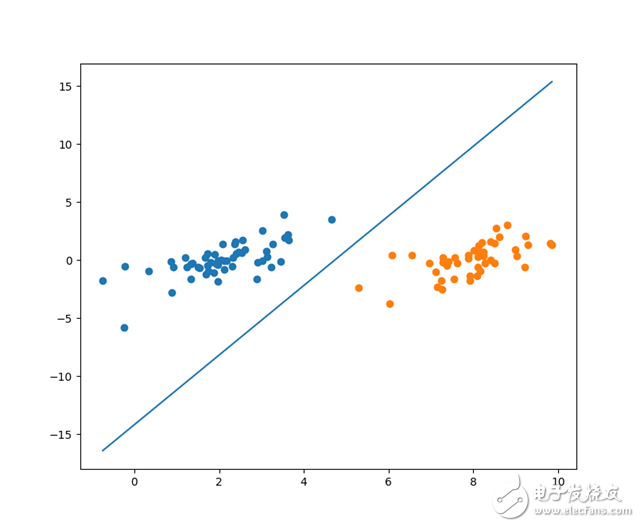
The resulting segmentation curve is shown below:
Connector 3.96Mm Pitch,Ressure Welding Bar Connector,Wire To Board Power Connector,Tcj6 Wire-To-Board Connector
YUEQING WEIMAI ELECTRONICS CO.,LTD , https://www.wmconnector.com